- Vulnerable: 1
- definitely endangered: 2
- severely endangered: 3
- critically endangered: 4
- extinct: 5Introduction
To quantify and ascertain whether social and economic factors affect the degree of language endangerment, two Bayesian linear models were built:
- Model A: Predict the numeric degree of language endangerment. The categories of language endangerment are converted to numbers, and a Bayesian Gaussian linear regression model is used to predict the numeric target:
- Model B: Predict the probability of language endangerment. With Model B, the plan is to predict the probability of an endangered language evolving up from one classification all the way to finally becoming extinct. A Bayesian ordinal logistic regression model is built to understand the orderly nature of moving across the degrees (or severity) of language endangerment.
The social and economic factors explored are:
- literacy: Literacy Rate of the Country
- infant_mortality: Infant Mortality Rate of the Country
- agriculture: Percentage of GDP that is made up of Agriculture
- proximity_to_capital_city: How close is the region in which the language is spoken to the capital city?
- minority_ed_policy: Does the country have any policies to foster education in minority languages?
- urban_pop_pc_change_1960_2017: Urban population change between 1960 to 1970
Model A: Predict Numeric Degree of Endangerment
\[ \begin{aligned} \operatorname{degree\_of\_endangerment\_numeric} &= \alpha + \beta_{1}(\operatorname{literacy})\\ &\quad + \beta_{2}(\operatorname{infant\_mortality}) + \beta_{3}(\operatorname{agriculture})\\ &\quad + \beta_{4}(\operatorname{proximity\_to\_capital\_city}) + \beta_{5}(\operatorname{minority\_ed\_policy})\\ &\quad + \beta_{6}(\operatorname{urban\_pop\_pc\_change\_1960\_2017}) + \epsilon \end{aligned} \]
Assessing Model
| Term | Median | Lower Limit | Upper Limit | Is Significant? |
|---|---|---|---|---|
| (Intercept) | 0.594 | −0.970 | 2.145 | No |
| literacy | 0.677 | −0.686 | 2.076 | No |
| infant_mortality | 0.025 | 0.000 | 0.050 | No |
| agriculture | −2.300 | −7.844 | 3.066 | No |
| proximity_to_capital_city | 0.388 | 0.076 | 0.702 | Yes |
| minority_ed_policy | 0.441 | −0.076 | 0.952 | No |
| urban_pop_pc_change_1960_2017 | 0.023 | 0.002 | 0.044 | Yes |
\[ \begin{aligned} \operatorname{\widehat{degree\_of\_endangerment\_numeric}} &= 0.595 + 0.678(\operatorname{literacy})\\ &\quad + 0.025(\operatorname{infant\_mortality}) - 2.300(\operatorname{agriculture})\\ &\quad + 0.388(\operatorname{proximity\_to\_capital\_city}) + 0.441(\operatorname{minority\_ed\_policy})\\ &\quad + 0.023(\operatorname{urban\_pop\_pc\_change\_1960\_2017}) \end{aligned} \]

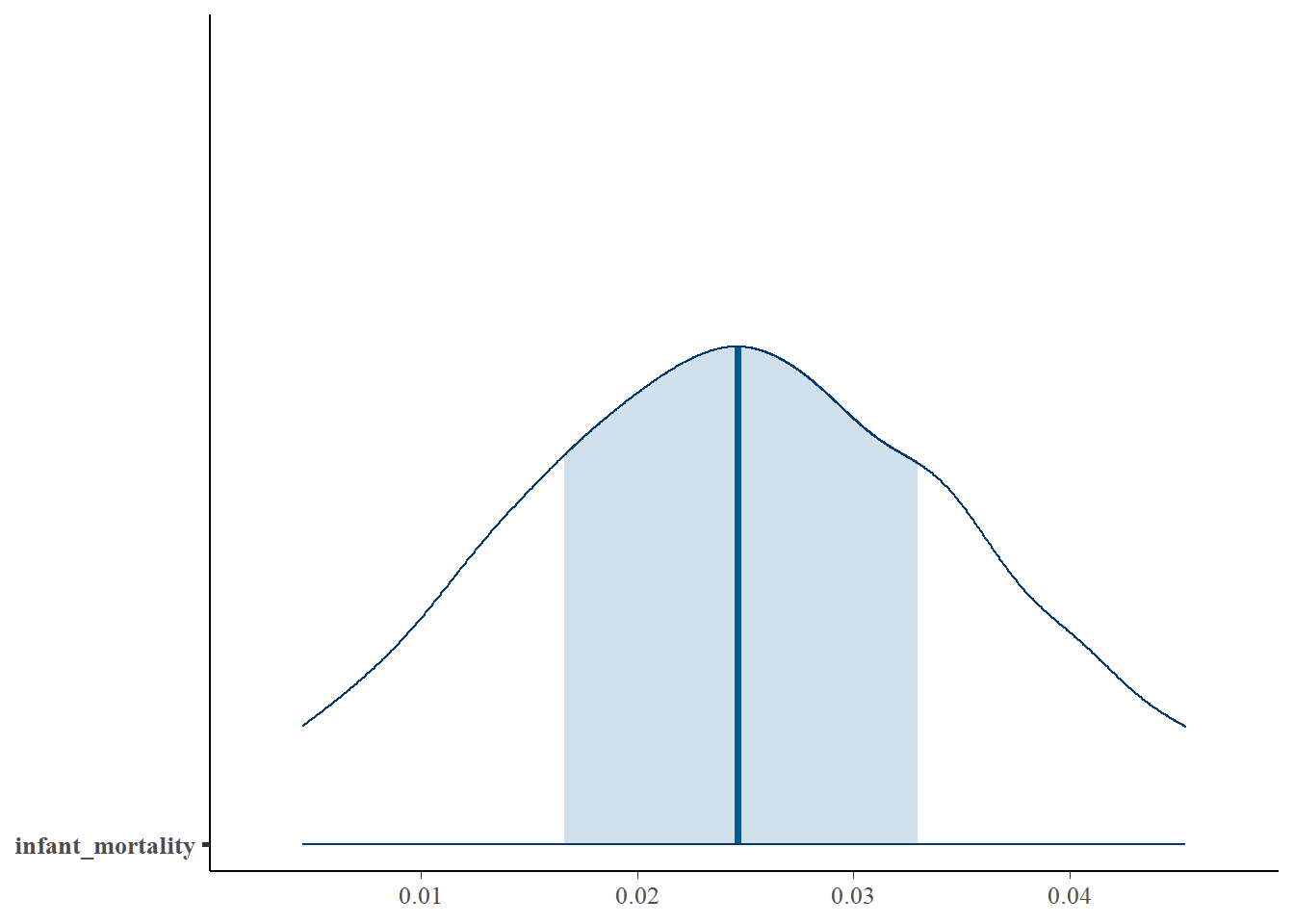
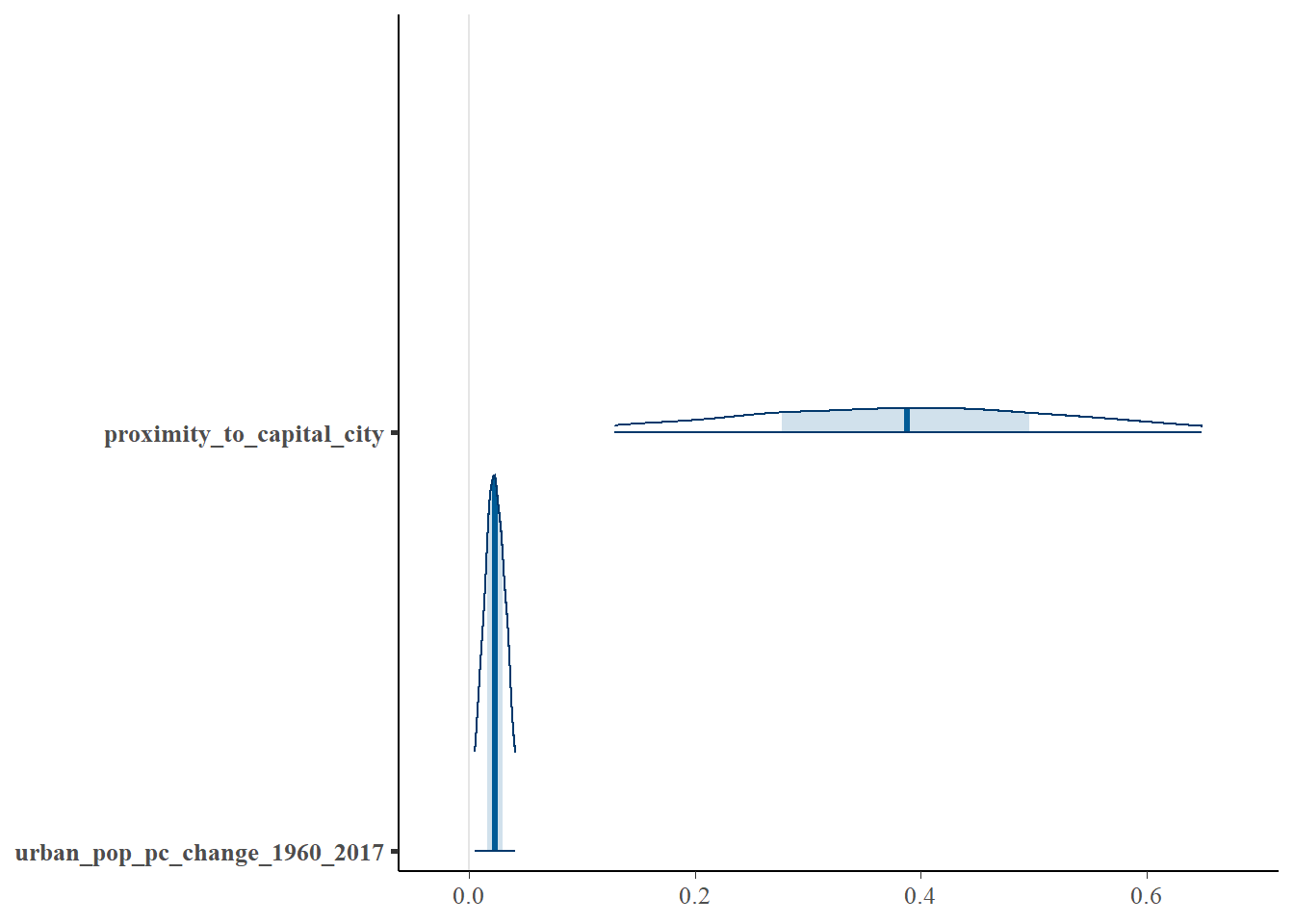
Key Discoveries
Urbanization further endangers languages.
- When an endangered language is close to an urban center it’s more likely to go extinct
- As migration to urban centers increase, languages become increasingly endangered
- Other social and economic factors do not seem to impact degree of endangerment when urbanization is considered
Model B: Predict Probability of Degree of Endangerment
\[ \begin{aligned} \operatorname{\phi} &= \beta_{1}(\operatorname{literacy})\\ &\quad + \beta_{2}(\operatorname{infant\_mortality}) + \beta_{3}(\operatorname{agriculture})\\ &\quad + \beta_{4}(\operatorname{proximity\_to\_capital\_city}) + \beta_{5}(\operatorname{minority\_ed\_policy})\\ &\quad + \beta_{6}(\operatorname{urban\_pop\_pc\_change\_1960\_2017}) \end{aligned} \]
\[ \begin{aligned} \log\left[ \frac { P( \operatorname{vulnerable} \geq \operatorname{definitely\ endangered} ) }{ 1 - P( \operatorname{vulnerable} \geq \operatorname{definitely\ endangered} ) } \right] &= \alpha_{1} - \phi + \epsilon \\ \log\left[ \frac { P( \operatorname{definitely\ endangered} \geq \operatorname{severely\ endangered} ) }{ 1 - P( \operatorname{definitely\ endangered} \geq \operatorname{severely\ endangered} ) } \right] &= \alpha_{2} - \phi + \epsilon \\ \log\left[ \frac { P( \operatorname{severely\ endangered} \geq \operatorname{critically\ endangered} ) }{ 1 - P( \operatorname{severely\ endangered} \geq \operatorname{critically\ endangered} ) } \right] &= \alpha_{3} - \phi + \epsilon \\ \log\left[ \frac { P( \operatorname{critically\ endangered} \geq \operatorname{extinct} ) }{ 1 - P( \operatorname{critically\ endangered} \geq \operatorname{extinct} ) } \right] &= \alpha_{4} - \phi + \epsilon \end{aligned} \]
Assessing Model
| Term | Median | Lower Limit | Upper Limit | Is Significant? |
|---|---|---|---|---|
| literacy | 0.816 | −1.149 | 2.775 | No |
| infant_mortality | 0.031 | −0.004 | 0.070 | No |
| agriculture | −3.189 | −11.713 | 4.913 | No |
| proximity_to_capital_city | 0.433 | −0.016 | 0.904 | No |
| minority_ed_policy | 0.683 | −0.050 | 1.442 | No |
| urban_pop_pc_change_1960_2017 | 0.031 | 0.002 | 0.066 | Yes |
| vulnerable|definitely endangered | 1.009 | −1.246 | 3.281 | No |
| definitely endangered|severely endangered | 2.551 | 0.263 | 4.888 | Yes |
| severely endangered|critically endangered | 4.037 | 1.613 | 6.525 | Yes |
| critically endangered|extinct | 6.109 | 3.410 | 9.086 | Yes |
\[ \begin{aligned} \operatorname{\hat{\phi}} &=0.816(\operatorname{literacy})\\ &\quad + 0.031(\operatorname{infant\_mortality}) - 3.189(\operatorname{agriculture})\\ &\quad + 0.433(\operatorname{proximity\_to\_capital\_city}) + 0.683(\operatorname{minority\_ed\_policy})\\ &\quad + 0.031(\operatorname{urban\_pop\_pc\_change\_1960\_2017}) \end{aligned} \]
\[ \begin{aligned} \log\left[ \frac { P( \operatorname{vulnerable} \geq \operatorname{definitely\ endangered} ) }{ 1 - P( \operatorname{vulnerable} \geq \operatorname{definitely\ endangered} ) } \right] &= 1.009 - \hat{\phi}\\ \log\left[ \frac { P( \operatorname{definitely\ endangered} \geq \operatorname{severely\ endangered} ) }{ 1 - P( \operatorname{definitely\ endangered} \geq \operatorname{severely\ endangered} ) } \right] &= 2.551 - \hat{\phi} \\ \log\left[ \frac { P( \operatorname{severely\ endangered} \geq \operatorname{critically\ endangered} ) }{ 1 - P( \operatorname{severely\ endangered} \geq \operatorname{critically\ endangered} ) } \right] &= 4.037 - \hat{\phi} \\ \log\left[ \frac { P( \operatorname{critically\ endangered} \geq \operatorname{extinct} ) }{ 1 - P( \operatorname{critically\ endangered} \geq \operatorname{extinct} ) } \right] &= 6.109 - \hat{\phi} \end{aligned} \]
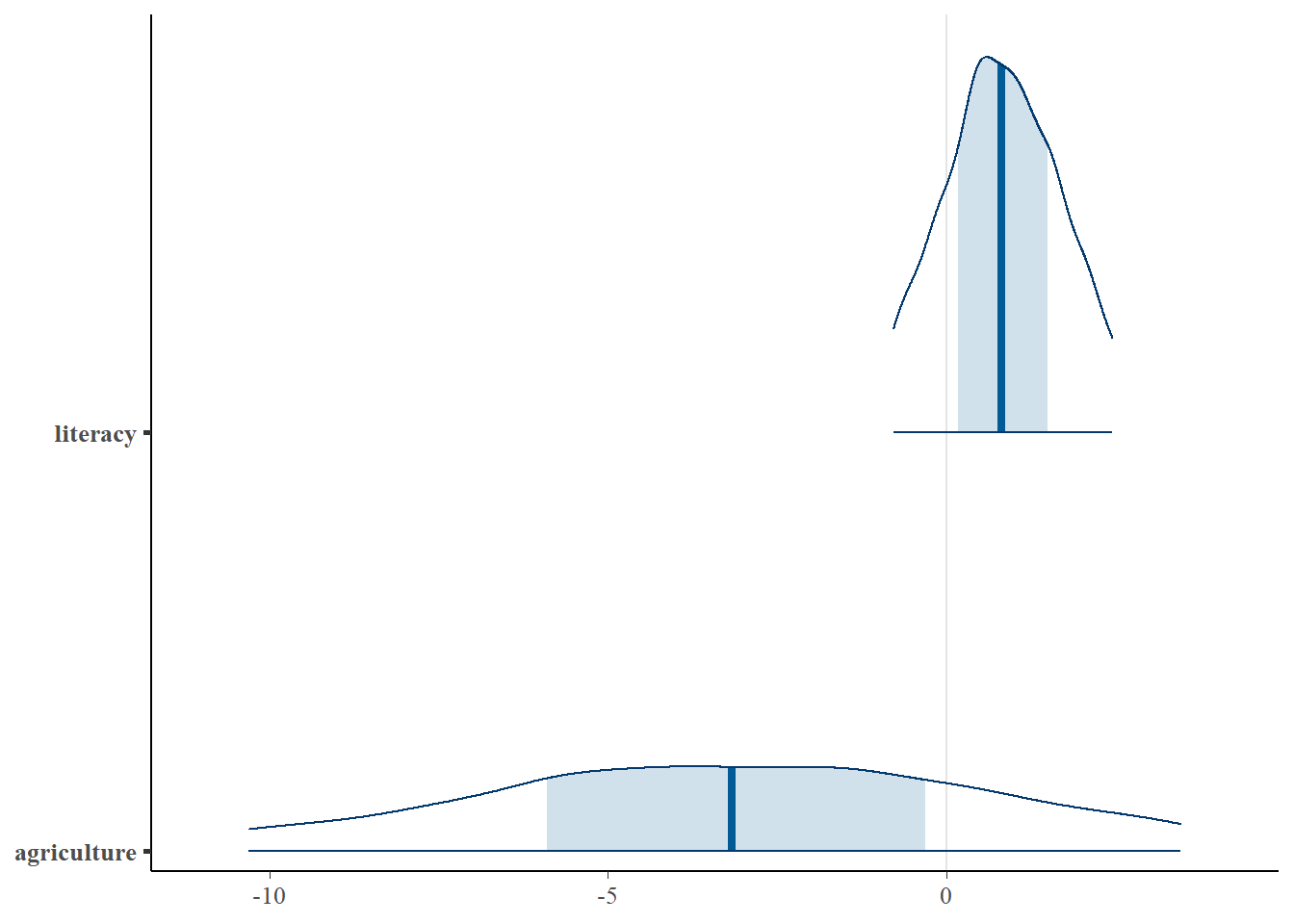
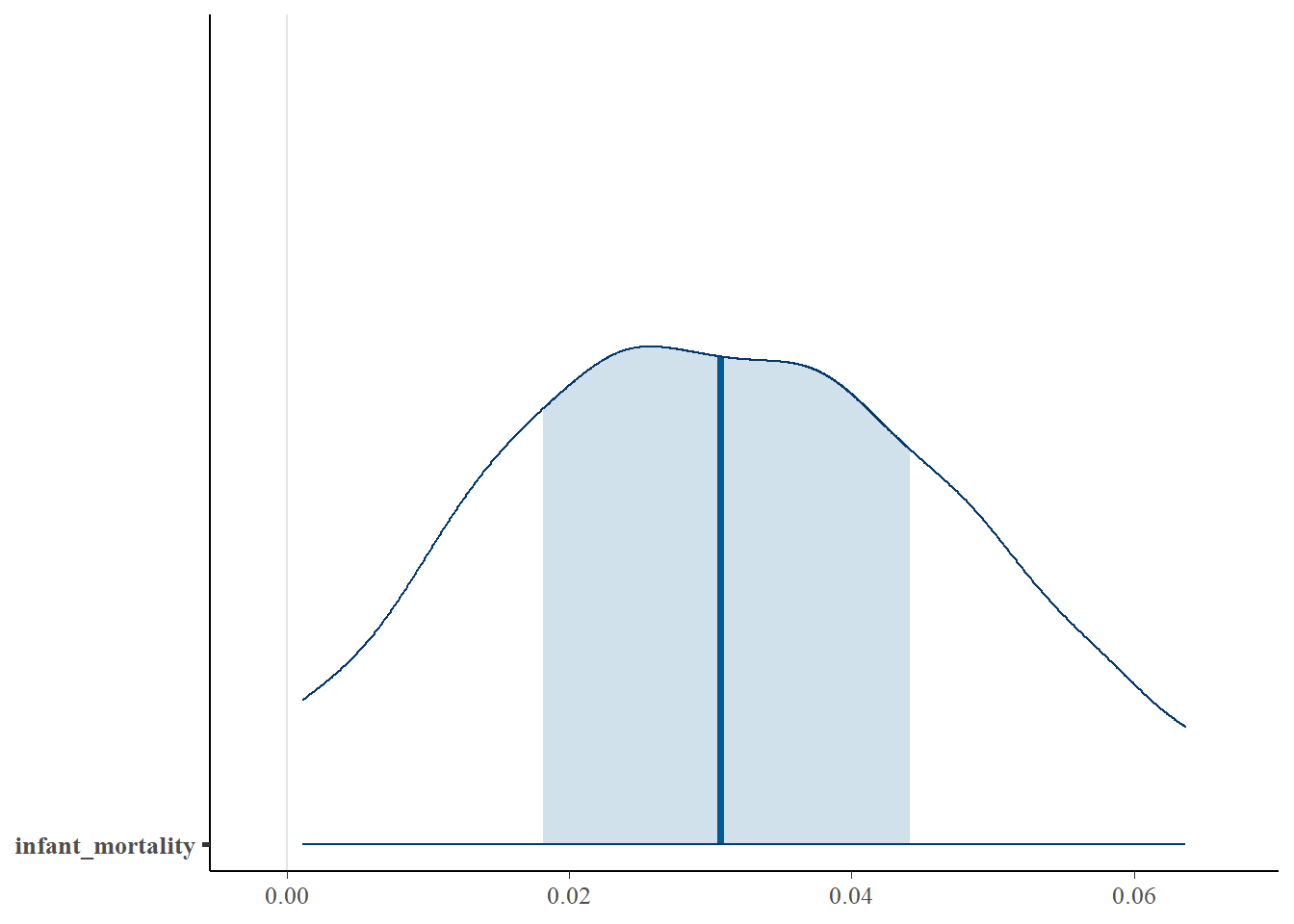
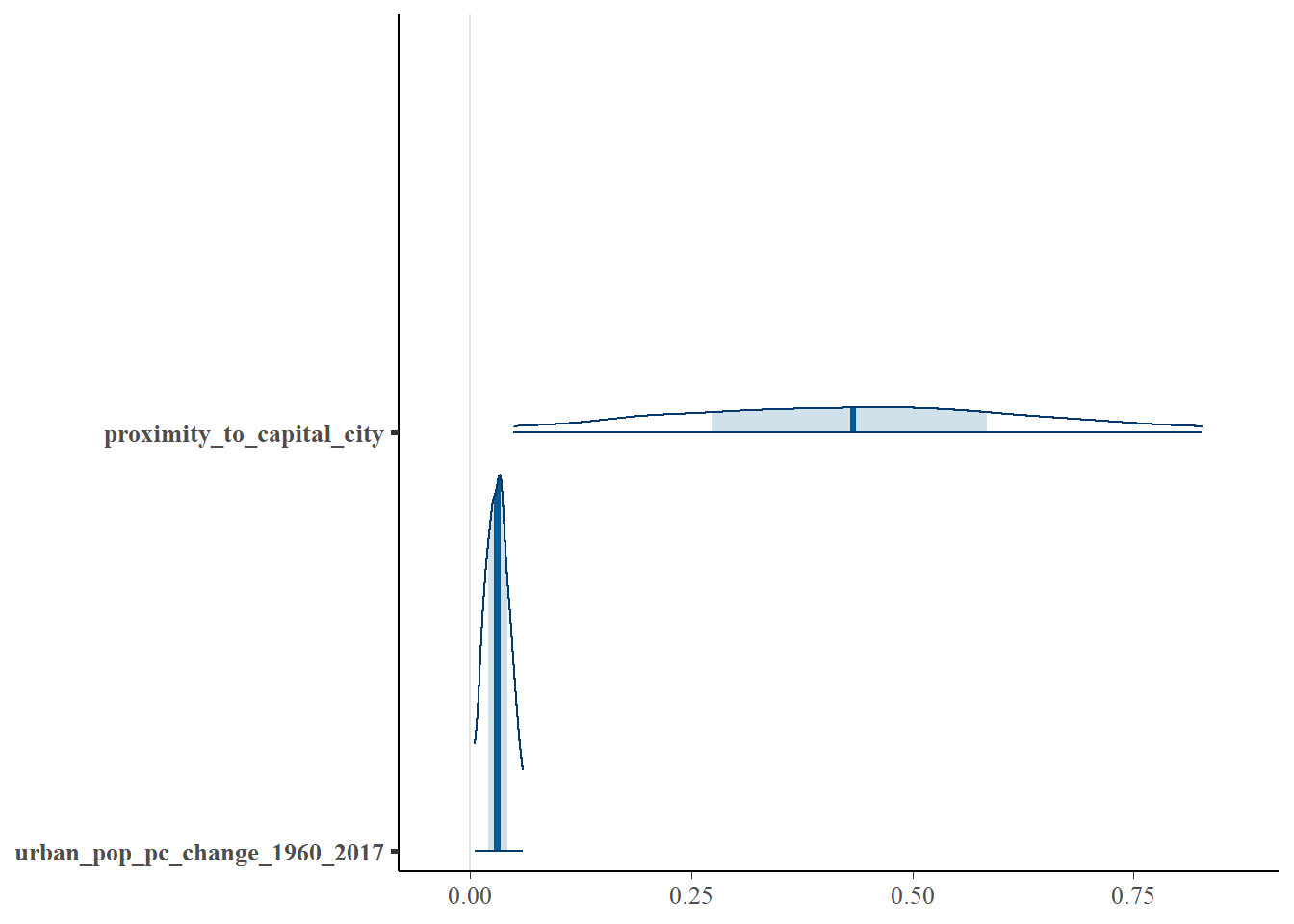
Key Discoveries
Urbanization increases the odds of language endangerment.
- When an endangered language is close to an urban center it’s more likely to go extinct
- As migration to urban centers increase, languages become increasingly endangered
- Other social and economic factors do not seem to impact degree of endangerment when urbanization is considered
The following movements in the severity of language endangerment are also very significant:
- A language that is classified as definitely endangered is at a significant risk of becoming severely endangered
- A language that is classified as severely endangered is at a significant risk of becoming critically endangered
- A language that is classified as critically endangered is at a high significant risk of becoming extinct
Conclusion
To help preserve endangered languages, policy makers must introduce policies that make endangered regions more attractive to prevent migration of current speakers to urban regions.
Also improving literacy rate and agricultural economic opportunities in these regions could help preserve the local population, and in turn preserve the local language.
Languages that are already classified as definitely endangered are at significant risk of going extinct. Urgent attention should be given to such languages.